一、系统设计与精度评估
1、 系统设计
本研究中使用的三维数字图像相关(3D-DIC)系统由两台工业相机(IDS UI-3370CP,2048×2048像素CMOS传感器)和一台投影仪(DLP Light Crafter 4500评估模块)组成,如图1a所示。投影仪投射数字相关计算所需的散斑图像,两台工业相机构成一个立体视觉系统,用于3D-DIC重建。编码点通过15位同心圆进行编码。一台单反相机(NIKON D7100,6000×4000像素CMOS传感器)用于近距离摄影测量,以重建编码点的三维空间坐标。工业相机配备有C口50mm定焦镜头(KowA-LM50XC,50mm,4/3英寸),单反相机则使用尼康50mm定焦镜头(50mm F/1.4g)。3D-DIC系统的物距约为1米,视场约为160×160毫米,立体视角为35度。在本研究中,使用团队开发的内部软件(如图1b所示)进行3D-DIC计算和编码点重建。
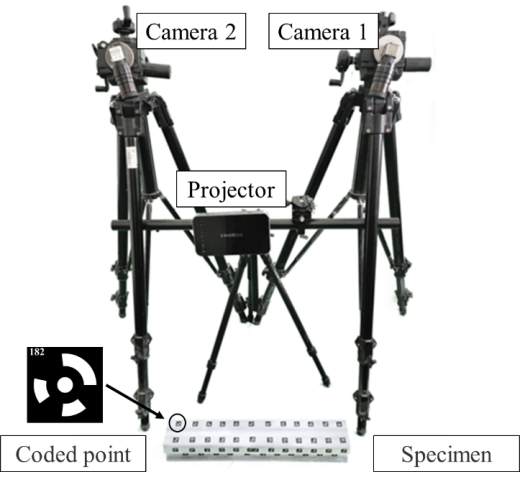
(a)带有投影仪系统的三维数字图像相关
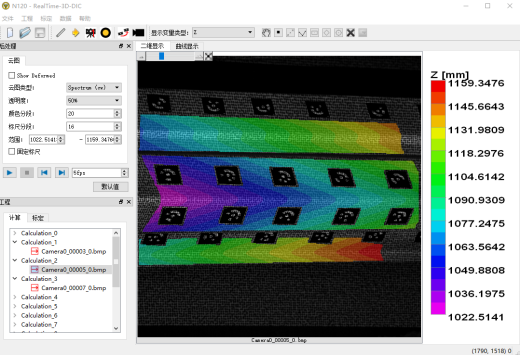 | 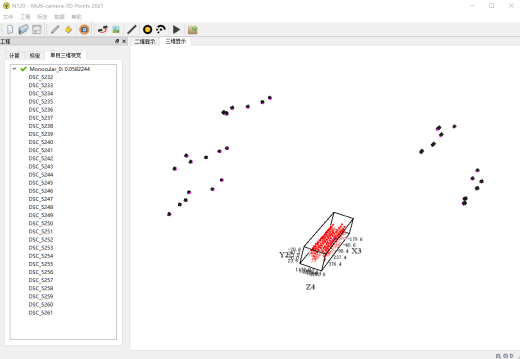 |
| 3D-DIC 软件 | 3D点云重建软件 |
(b)测量软件
图1 带有投影仪系统的三维数字图像相关
2、圆柱管的精度评估
3D-DIC(三维数字图像相关)测量的精度不仅高度依赖于设备的精度,还依赖于重建算法的准确性。在本节中,首先通过一个简单的圆柱构件验证该方法在几何缺陷测量中的精度,然后再将其应用于更复杂的构件。首先,3D-DIC系统本身的精度可以达到±0.0016 mm。其次,点云拼接的精度还会受到编码点识别精度的影响。这些因素共同决定了测量的精度,例如本研究中几何缺陷的测量精度。
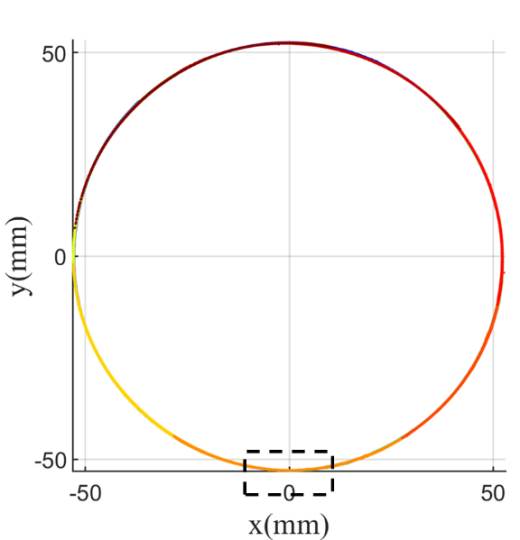
使用一个直径为106 mm、长度为280 mm的圆柱管进行了验证测量。编码点布置在管的外表面,如图2(a)所示。带有编码点的试件通过单反相机从多个角度进行拍摄,然后使用近距离摄影测量技术重建编码点的空间坐标并建立全局坐标系,如图2(b)所示。随后,通过移动试件获取几何形态点云,每个局部点云覆盖试件约20%的周长。基于立体视觉原理计算局部坐标系中编码点的坐标数据,并将试件的全场点云拼接完成。将每个点云点的半径转换为圆柱坐标。全场点云的半径R如图2(c)所示,其中空白区域对应编码点。总体而言,与理想几何形状相比,计算半径R的标准偏差为0.0739。在图3所示的拼接区域(矩形区域x),点云1和点云2(即旋转试件前后的两组测量数据)非常接近。因此,本研究中使用的方法的全局精度约为±0.1 mm(厚度的5%),满足精度要求。
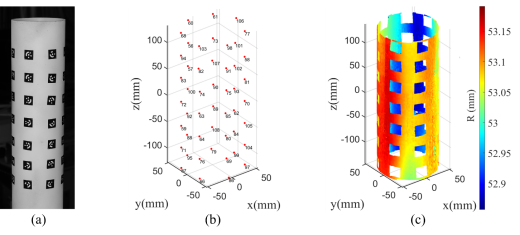
图2 精度分析测试与可视化:a) 带有编码点的圆柱管 b) 编码点的全局坐标 c) 测量的半径R结果
 | 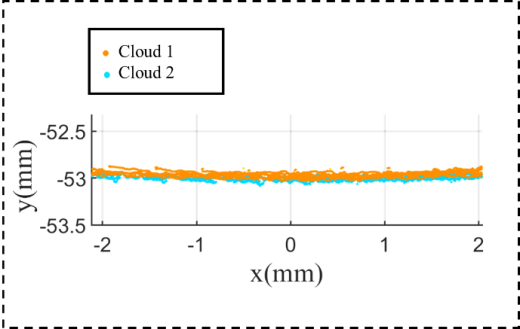 |
(a) 矩形区域内显示拼接区域的横截面 | (b) 测量的点云半径R |
图3 点云拼接(俯视图):a) 矩形区域内显示拼接区域的横截面 b) 拼接区域内测量的点云半径R
二、货架立柱的几何形态测量
1、如前所述,所开发的3D-DIC系统在几何缺陷测量中的精度在可接受范围内。因此,该系统被应用于测量更复杂截面的缺陷:一种钢制仓储货架立柱。如图4所示,该截面包含多个弯折和加强筋。截面尺寸为Ω120×85×2.0 mm,由Q235B(即屈服应力fy = 235 MPa)钢板通过折弯成型。试件长度为600 mm,无穿孔。需要注意的是,由于切割工艺,试件两端存在明显的局部几何缺陷。
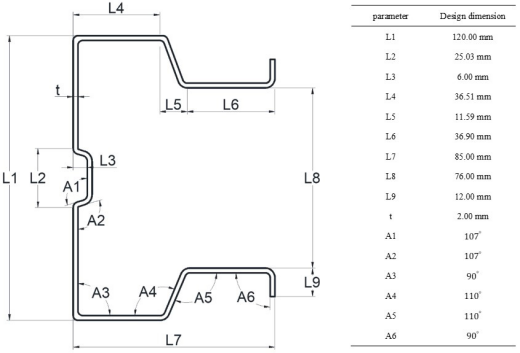
(a)钢制货架立柱的设计截面(单位:mm)

(b)测试试件
图4 钢制货架立柱:(a) 钢制货架立柱的设计截面(单位:mm) (b) 测试试件
由于截面具有多个弯折,其表面无法通过单次相机拍摄完成测量,原因是视线遮挡以及相机视野范围的限制。因此,为了完整测量试件的几何形态,采用了多次拍摄的方式。如图5所示,通过固定3D-DIC系统和投影仪,旋转试件4次以获得环形区域的几何形态。随后,将试件沿纵向平移至新的测试区域,继续进行下一个环形区域的测量。特别地,为了确保没有未测试的区域,每个新的测试区域需要与上一个区域有少量重叠。由于试件长度为600 mm,而相机视野范围为160×160 mm,因此需要进行4次平移,共拍摄16组图像。通过3D-DIC计算,获得了16组局部坐标系下的试件几何形态,如图5(b)所示。此外,如图5(c)所示,通过近距离摄影测量技术重建的全局坐标系与局部坐标系中的编码点结合,计算得到刚体变换矩阵Hi。利用这些刚体变换矩阵,将点云数据统一到全局坐标系中,最终实现试件的全场几何形态重建,如图6所示。
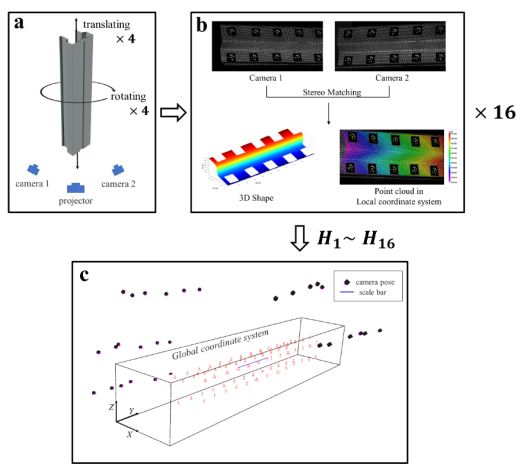
图5 测量流程
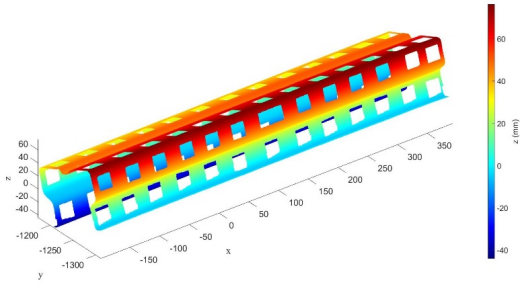
图6 三维重建结果(单位:mm)
2、立柱的初始几何缺陷
为了获取试件的几何缺陷,需要将测量的点云数据(使用中间580 mm的点云数据进行初始几何缺陷计算和建模)与构件的设计值(即理想化的完美几何形状)进行比较。采用迭代最近点算法(ICP) 将实测点云数据与理想几何点云进行配准。使用的目标函数如下:
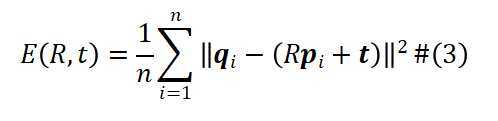
其中,qi 和 pi 分别是理想几何点云和实测点云的坐标,R和t分别是从实测点云到理想几何点云的旋转矩阵和平移向量。
配准后的点云是与理想几何点云差异最小的点云。配准后,两组点云之间的差异即为试件的几何缺陷。在使用ICP算法进行点云配准时,每个截面有329个点,沿构件长度方向共有580个截面。两组点云数据的ICP配准结果如图7所示。
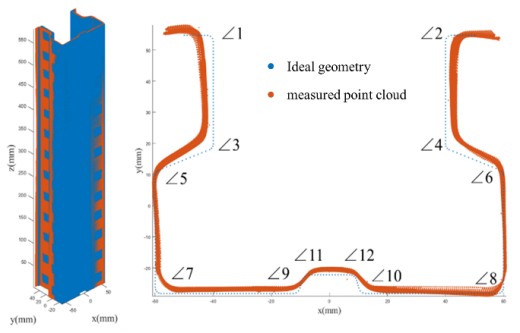
图7 ICP配准结果